ARCHIMEDES' PRINCIPLE AND LAW OF FLOTATION

Archimedes' principle indicates that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially submerged, is equal to the weight of the fluid that the body displaces. Archimedes' principle is a law of physics fundamental to fluid mechanics.

The Concept of Upthrust

Explain the concept of upthrust

If a heavy object is lifted while immersed in water, it may be raised more easily than when outside the water. This is due to the reason that when anything is placed in liquid, it receives an upward force called upthrust. A body appears to have lost some weight when immersed in water due to the upthrust exerted on the body by the water.

• By definition upthrust is referred as an upward force exerted by the body when it’s partially or totally immersed in water.
• Consider the experiment below to verity the concept of upthrust.

From this experiment, it will be observed that W1>W2. This is because:

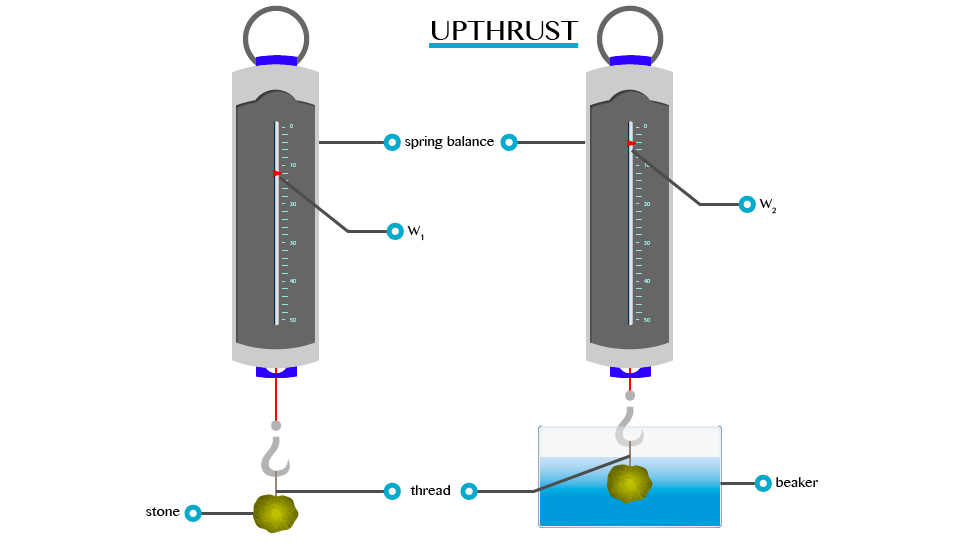
When a body is partially or totally immersed in any liquid, the liquid exerts an upward force.

A weight recorded on the spring balance of a body that is totally or partially immersed in any liquid is called apparent weight. E.g. W2 and the force, which temporally reduces the weight of the body, are called upthrust (u).

Verification of the Archimedes' Principle

Verify the archimedes principle

This is the principle which shows the relationship between the upthrust acting on a body and the weight of fluid it displaces when partially or completely immersed in the fluid. It was first discovered by a Greek scientist called Archimedes (287 to 121 BC).

• The principle states that, ”when a body is partially or totally immersed in a fluid it experiences an upthrust which is equal to the weight of the fluid displaced.”
• This principle can be verified by the following experiment.

Results:Weight of a body in air = W1

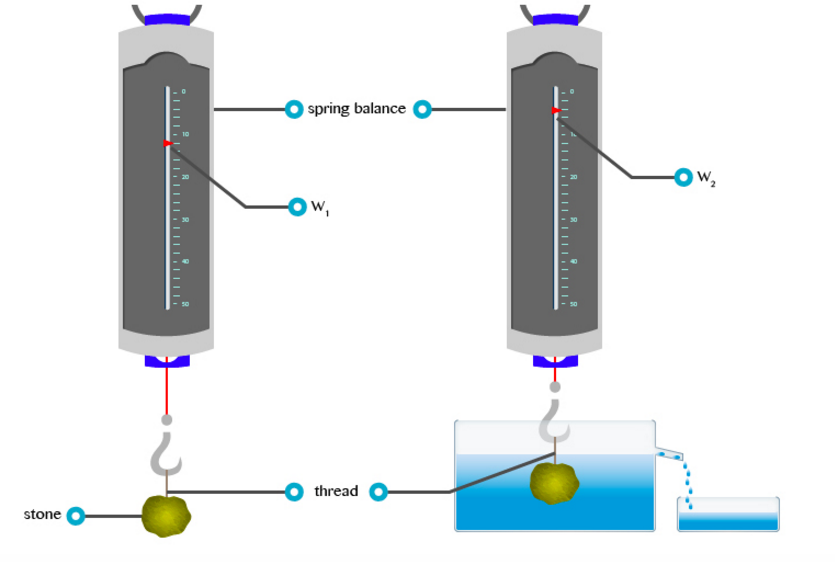
Verification of the Archimedes' Principle

Weight of a body in water = W2 (apparent weight)

Uptrust = Loss of weight in water

U = W1 –W2

Example 1

Weight of a body in air = 10.0N

Weight of a body when immersed in water = 9.2N find the upthrust.

Solution:

Data given

Weight of a body in air (W1)= 10.0N

Weight of a body when in water (W2) = 9.2N

Formula

Upthrust = Loss of weight in water = W1-W2

= 10.0N – 9.2N

= 0.8N

The upthrust is 0.8

Example 2

The weight of a body when totally immersed in liquid is 4.2N. if the weight of the liquid displaced is 2.5N, find the weight of the body in the air.

Solution;

Data;

Apparent weight (W2) = 4.2N

Weight of liquid displaced (u) = 2.5N

Weight of body in air=?

Formular;

U = W1 –W2

W1= 4.2 +2.5 = 6.7N

Weight of body in air is 6.7N

The Archimedes' Principle in Determining Relative Density

Apply the archimedes principle to determine relative density

Relative density (R.D) of a substance can be defined as a ratio of the mass of a certain volume of the substance to the mass of an equal volume of water.

Relative density = Mass or weight of given volume of a substance overMass or weight of an equal volume of water.

R.D = weight of a substance in air over Weight of displaced water.

R.D = weight of a substance in air

From Archimedes’ principle the weight of an equal volume of water is equal to the weight of water displaced by the object, which is equal to the upthrust loss in weight. By weighing an object in air and then in water, the relative density can be determined.

Weight of a body in air = W1

Weight of a body in water = W2

Apparent loss in weight = W1-W2

Relative density = W1/W1 - W2

Example 3

A piece of glass weigh 1.2N in air and 0.7N when completely immersed water. Calculate its:

1. Relative density
2. Density of a glass

Given that density of water = 1000kg/cm3

And acceleration due to gravity = 10N/kg

Solution

Weight of the glass in air (W1) = 1.2N

Weight of the glass in water (W2) = 0.7N

R.D = W1/W1 – W2

1.2N/(1.2 – 0.7)

1.2/0.5

R.D = 2.4

R.D = Density of glass/Density of water

Density of a glass = R.D x Density of water

= 2.4 x 1000kg/cm

= 2400kg/m3

NB: Relative density has no SI unit

Law of Flotation

Difference between Floating and Sinking of Objects

Distinguish floating and sinking of objects

As we have discussed in upthrust, different objects with different density can sink or float. The object with higher density than water density will sink while that object with a density lower than water’s density will float. For example, a coin sinks in water and a large ship floats on water.

The Conditions for a Substance to Float in Fluids

Explain the conditions for a substance to float in fluids

When an object is completely or partially immersed in fluids, there are two forces acting on it, the weight (W) acting downwards and the upstrust (u) acting upwards. Refer to the figure below:

Conditions

Conditions for a body to float include:

1. If W>U, there is downward movement of the body which is termed as sinking.
2. If W<U, there is upward movement of the body.
3. If W=U, the body is equilibrium under the action of two equal and opposite force. Thus, the body floats.

Relationship between Upthrust and Weight of Floating Body

Relate upthrust and weight of floating body

The relationship can be determined by considering the following experiment.

Upthrust and Weight of Floating Body

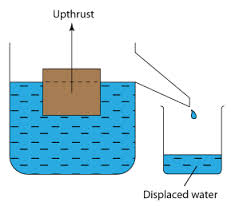
Principle of Floatation

State the law of flotation

The above experiment shows that, the upthrust is equal to the weight of the liquid displaced and therefore the upthrust is equal to the weight of the floating body as the two forces are equal.

The mass of the floating body is equal to the mass of fluid displaced; in the above experiment is the same as the weight of the piece of wood. This result is agreement with the principle of floatation.

The principle of floatation states “A floating body displaces a weight of the fluid which is equal to its own weight.”

The Law of Floatation in Everyday Life

Apply the law of flotation in everyday life

Floating of ship

Iron is much denser than water and a block of iron sinks immediately in water. Ships are made with hollowness such that their total densities are less than that of water. Therefore, a ship displaces water equal to its weights.

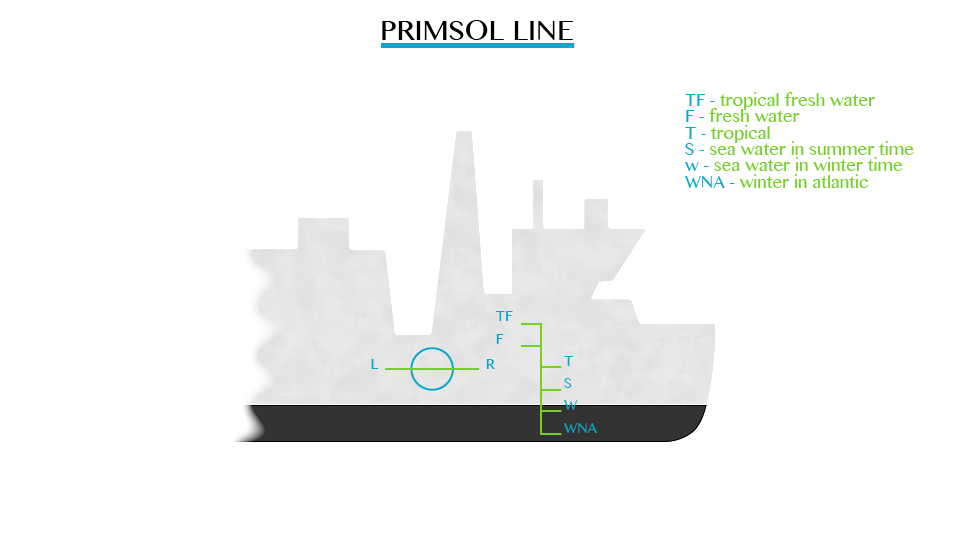
The upthrust of the water is sufficient to support the weight of the ship. When the ship is loaded with cargo it sinks lower in the water. The volume of water displaced by the ship and its cargo depends upon whether it is floating in fresh water or in seawater. It floats lower in fresh water (R.D= 1.0) than in seawater (R.D=1.025) the mass of fresh water displaced.

For example, if a ship weighs 20,000 tons, then it must displace 20,000 tones of water to float. If 2,000 tones of cargo is added, the ship lowers in water until an extra 1,000 tons of water have been displaced

Plimsoll line;This line indicates the safe limit of loading. Many plimsoll lines may be marked on a ship to show minimum heights above different types of water in different seasons.

Balloons

Figure below shows the type of balloons used to carry instruments to a high altitude for recording meteorological measurements when filled with gas. E.g. helium, it displaces a volume of air equal to its volume.

Air has greater density compared to the density of a gas in the balloon. Therefore, the weight of air displaced is greater than that of balloon. The balloon drifts up by a force, which is equal to the difference between the upthrust and the total weight of the balloon (W).

Submarine

The buoyancy of a submarine depends on the quantity of water in its ballast tanks. When it is required to drive, water is admitted to special tanks. When the water is ejected from the tanks by means of compressed air, the submarine raises to the surface and floats just like any other ship.

The mode of Action of a Hydrometer

Describe the mode of action of a Hydrometer

A hydrometer is an instrument used for measuring the densities of liquids such as milk, alcohol and acids. The greater the density of the liquid the shorter the stem of hydrometer immersed. Hydrometer sinks lower in kerosene and floats higher in water.

Construction of a Simple Hydrometer

Construct a simple Hydrometer

Single hydrometer can be made using pieces of straws or test tubes weighed down with wax.

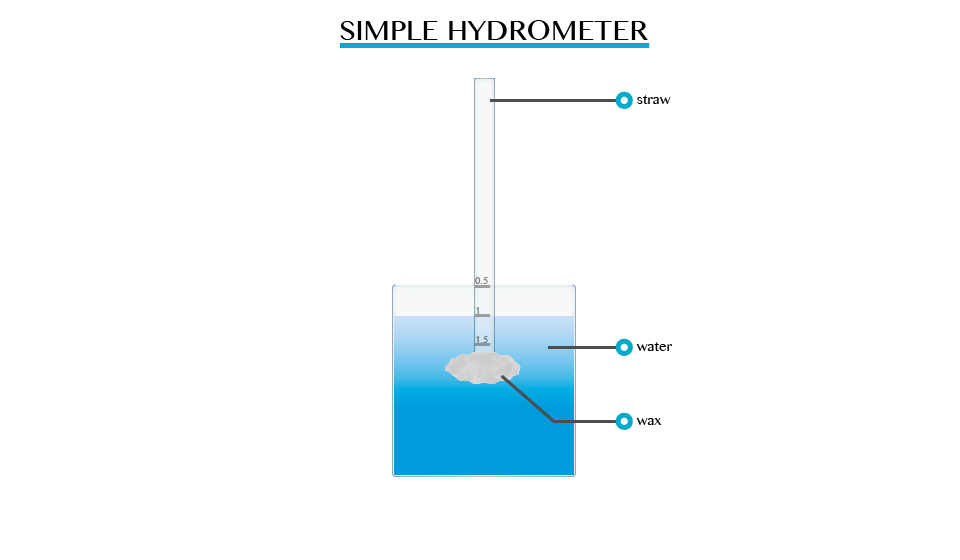
Hydrometer in Determining the Relative Density of Different Liquids

Use Hydrometer to determine the relative density of different liquids

The relative density of liquid is measured directly by using a suitable hydrometer, it contains:

1. A heavy sinker, containing mercury or lead shots that keep the hydrometer upright when it floats.
2. An air bulb to increase the volume of displaced liquid, and overcomes the weight of the sinker.
3. The stem is thin so that small changes in density give large differences in readings.
4. The hydrometer is made up of glass so it does not soak up liquids.

TOPIC 6: STRUCTURE AND PROPERTIES OF MATTER 

Structure of Matter

State of matter is defined in terms of the phase transitions which indicate the change in structure and properties. Solids, liquids and gases all are made up of microscopic particles. The behavior of all these particles also varies in three phases.

The Concept of Matter

Explain the concept of matter

Matter is anything, such as a solid, liquid or gas, that has weight (mass) and occupies space. For anything to occupy space, it must have volume.

The Particular Nature of Matter

Justify the particulate nature of matter

Matter is made up of tiny particles. The particles are atom or molecules, examples of substances, which are made up of atoms, are: gold, copper, Argon and silver; and those made up of molecules includes oxygen, water and ammonia.

• In solid, storm’s attractive forces hold molecules together so that they are not free to move but they can only vibrate about their mean positions.
• In liquids there are weak forces of attraction between molecules therefore the molecules are free to move randomly. The distances between molecules in liquids are therefore are larger than in solids.

In case of gases the molecules experience very weak forces of attraction and hence they are free to move randomly filling the whole space of the containing vessel. The distances between molecules in gases are comparatively greater than those in solids and liquids as shown in the figure above.

Demonstration to show the intermolecular space in solids, liquid and gases.

The Kinetic Theory of Matter

Explain the kinetic theory of matter

Generally, when solid particles are placed in the source of lead the particles tends to move from hot area to cold areas. These particles move because it gains energy that called it Kinetic energy.

Kinetic theory of matter sometimes attempts to explain how properties of gases like pressure, temperature and volume remain in constant motion.

There are three main parts of the Kinetic theory of matter. This includes:

1. Matter is made up of tiny invisible part.
2. Matter comes in different sizes.
3. There is a point that the smallest particles of matter can be the fastest.

Therefore kinetic theory of matter states, “All matter is composed of small particles”Or “Particles of matter are in steady motion and that all impacts between the units of matter are completely elastic”

Three States of Matter

Classify three states of matter

There are three states of matter, namely:

1. Solid state
2. Liquid state
3. Gaseous state

Solid state is the state of matter, which include solid materials, in which the intermolecular force between molecules are greatest and distance between molecules is small. Examples of solid state are wood, iron, etc.

Liquid sate is the one of the state of matter in which the intermolecular forces are low compared to solid state, there is greater distance between one molecule and another. See on figure 1.0 (b) examples water, soda, kerosene, and petroleum.

Gaseous state is the state of matter in which there is no intermolecular forces between molecules hence molecules are free to move from one place to another examples of gases are hydrogen, oxygen, carbon dioxide gas.

Difference between solid state, liquid state and gaseous state of matter

Solid state	Liquid state	Gaseous state.
It concerns with solid matter	It concerns with liquids/ fluids matter	It concerns with gases
Have high intermolecular	Low intermolecular force	No intermolecular force
No distance between molecules	There is little distance between molecules	Molecules are far from each other
Good examples are iron materials, woods etc.	Good examples are water, soda, kerosene and petrol	Good examples are oxygen and hydrogen

Rownian Movement

According to Robert Brown: Brownian movement refers to the irregular motion of tiny particles suspended in fluid (liquid organs). Consider the demonstrationbelow

Robert Brown, an English Botanist, powered some pollen grain in water and observed that particles floating in the water were darting about.

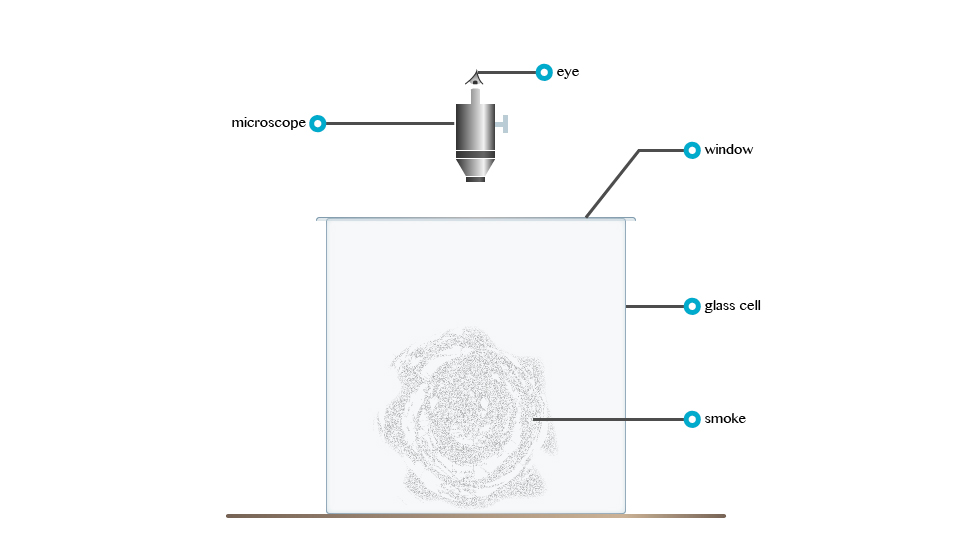
The irregular motion of tiny particles suspended in a fluid (fluid or gas) is called Brownian movement.

The tiny particles dart about because liquid molecules that are in state of motion bombard them.

Elasticity

The Concept of Elasticity

Explain the concept of elasticity

When a force is applied to a body the dimension of the body is usually altered. If an iron wire is stretched by small force applied to it longitudinally, the wire returns to its original shape and size when the force is removed.

Elasticity can be defined as the property of the iron wire by which it recovers its original shape and size on removal of the stretching force.

The Relationship between Tension and Extension of a Loaded Elastic Material

Justify the relationship between tension and extension of a loaded elastic material

Consider the graph below:

Point A is called the elastic limit. The straight region OA of the graph has a slope K given by the ratio.

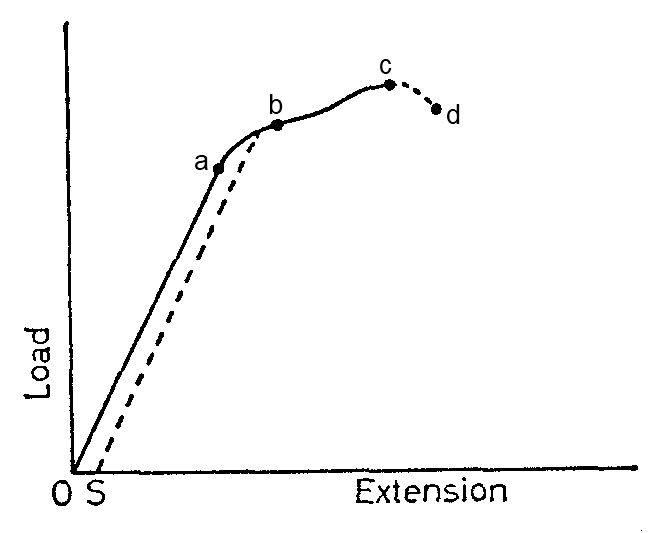
K= Tension/Extension

The ratio is called the force constant or coefficient of stiffness of the wire and it is expressed in newton per metre (N/M)

The Application of Elasticity in Real Life

Identify the applications of elasticity in real life

In everyday life we often actually do the activities that are concerned with the application of physics. Here are some of the application of physics in everyday life especially in the application of Elasticity:

• Spring mattress. When you sit or sleep on a spring mattress, futon style push your weight. Pressured by the compressed spring mattress. Due to the nature of its elasticity, stretch a spring mattress again. Spring will be stretched and compressed, and so on.
• Spring that is used as shock absorbers on motorcycles. Springs used in the suspension systems of motor vehicles. The purpose of this is to dampen spring a surprise when a motorcycle driven through an uneven road surface.
• Another simple example and that you may often come across is the catapult. When it was about to shoot birds with catapults for example, rubber slingshots first stretch (given the gravity). Due to the nature of its elasticity, long rubber slingshots will return to normal after a tensile force is removed.

Adhesion and Cohesion

The Concept of Adhesion and Cohesion

Explain the concept adhesion and cohesion

Matter is made up of molecules. That exerts force of attraction. This force of attraction may be either Cohesion or Adhesion.

• Cohesion is the force of attraction between the molecules of the same substance, example water to water molecules.
• Adhesion is the force of attraction between the molecule of different substances example water to glass molecules.

Water molecules can experience the force of cohesion among themselves, where water molecules and glass molecules will experience force of adhesion.

Definite shapes of a solid are due to strong cohesion force among its molecules.

Shapes and meniscus of a liquid

When we carried out activities involving determination of volume in a liquid ring and measuring cylinder. The description indicated that the surface of the liquid was carved, forming a meniscus, and that the volume must be read at the bottom or top of the meniscus, depending on the liquid used. For mercury, the top of the meniscus is read.

The formation of a meniscus in a liquid is due to forces of adhesion between the liquid and the walls of the container. The adhesion of the liquid such as water to the wall of a vessel causes an upward force on the liquid at the edge.

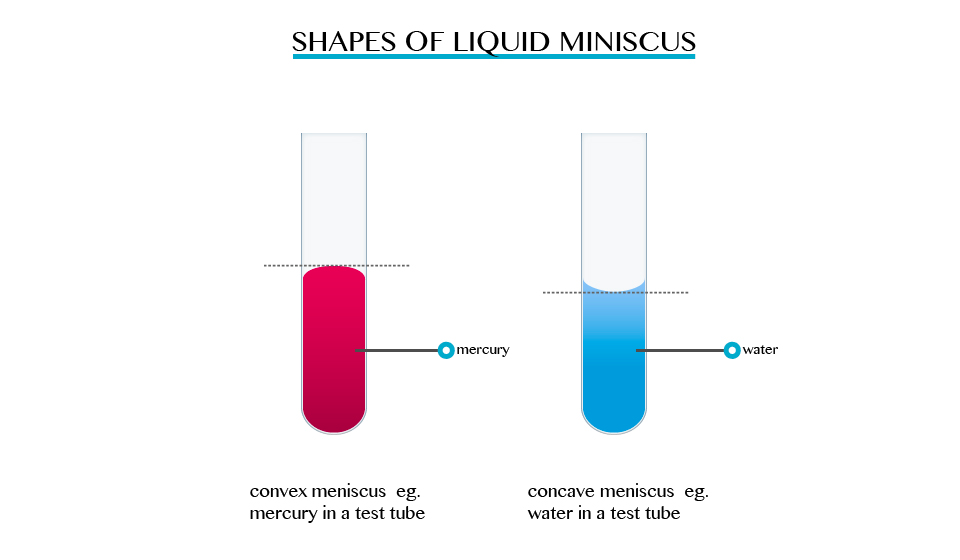
The opposite takes place in mercury, the meniscus of water curves upwards forming a concave shape. When a drop of each liquid, mercury and water are placed on a glass sheet, water spreads further unlike mercury, because of mercury’s high cohesion force among its particle.

Why water wets the glass?

Why methanol does not wet the glass?

Applications of Adhesion and Cohesion in Daily Life

Identify the applications of adhesion and cohesion in daily life

Application include the following

1. To stick two different objects together. Here we use the adhesive effects of tape or glue.
2. Adhesion can also be used to remove harmful materials such as bacteria from drinking water. Adhesive forces are the source attraction substance.
3. Cohesion assists in transport of water in plants and animals by allowing one molecule to pull others along with it.
4. The bodies of plants and animals also use the cohesion of tissue to repair damage.
5. Ink sticks on paper because of adhesive force between the paper and ink.

Surface Tension

The Concept of Surface Tension

Explain the concept of surface tension

While you may not be able to walk on water, water stride does. This is due to the property of liquid, which is known as surface tension.

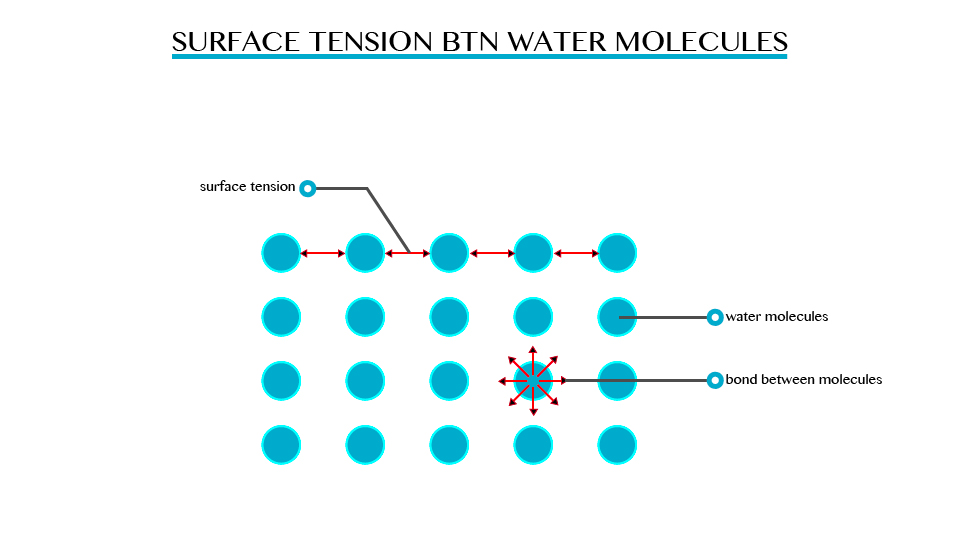
Surface tension is the ability of the molecules on the surface of a liquid to attract and stick to each other allowing them to resist an external force. Surface tension enables insects such as water strides and mosquitoes to walk on water. It allows small objects even metallic ones such as needles and razor blades to float on the surface of water.

Surface tension is a resultant attractive force between molecules in a liquid. The molecules below the surface liquid have forces of attraction between neighbouring particles. However molecules at the surface have no neighbouring molecules above them. This makes them have stronger attractive force than their nearest neighbours on the surface.

However, when some detergent is added to water, the same objects sink to the bottom of the trough. This means that the detergent interfered with the surface of the liquid so decreasing the tension of the water surface.

Detergents are example of surfactants. A surfactant is a substance that reduces the surface tension of a liquid.

Note: the term surfactant is an aerogun for surface-active agent.

Surface tension is affected by the following

• Nature of the liquid
• Contamination/impurities
• Temperature

Application at surface tension:

1. In extraction of impurities dating laboratory process.
2. Surfactants are also used to make emulsion of liquid like oil and water.
3. In cleaning action of soap.

Applications of Surface Tension in Daily Life

Identify the applications of surface tension in daily life

Application at surface tension

1. In extraction of impurities dating laboratory process
2. Surfactants are also used to make emulsion of liquid like oil and water.
3. In cleaning action of soap

Capillarity

The Concept of Capillarity

Explain the concept of capillarity

This is the tendency of a liquid to rise in narrow tubes or to be drawn into small openings such as those between the fibres of a towel. Capillarity can pull a column of liquid upward until the weight of liquid becomes greater than the surface tension.

In a tube, capillarity depends on the tube’s diameter but weight of water column depends on other factors besides it.

The smaller the radius of the tube the higher the liquid will rise in it. This implies that capillarity height is immensely proportional to the diameter of the tube.

By definition

Capillarity is defined as the tendency of liquid to rise in narrow tubes or to be drawn into small openings such as those between the fibres of a towel.

Capillarity action is the ability of a liquid to raise or fall in a narrow tube.

Note:

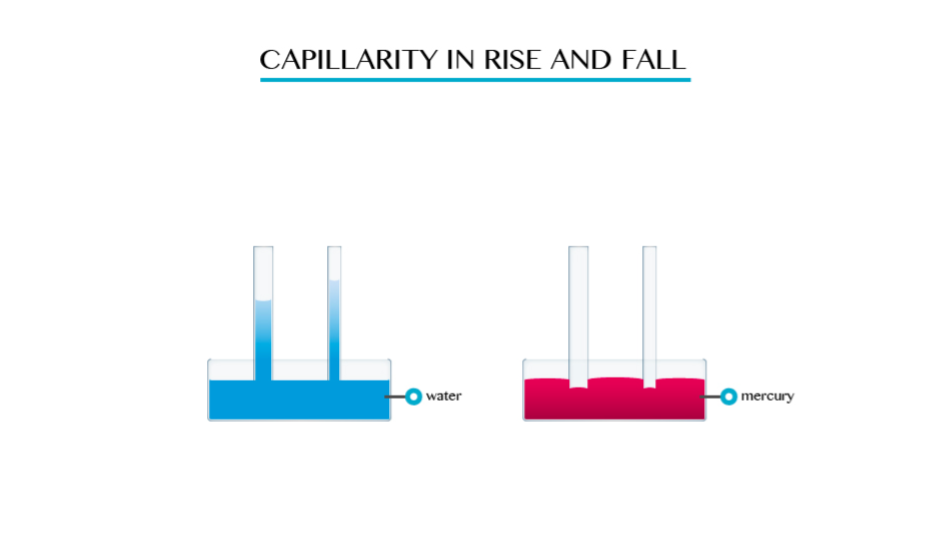
1. Capillarity depends on the type of liquid. For example if you dip capillarity tube in water the water rises in the tube and above the level of the water in the vessel.
2. If the tube is dipped in mercury, the liquid does not rise in the tube. It suffers capillarity depression.

Applications of Capillarity in Daily Life

Identify the applications of capillarity in daily life

The application includes:

1. Capillarity is essential to plants and animals.
2. In plants, it facilitates the transport of water and nutrients from the roots to the leaves where photosynthesis produces the plants food. In animals it assists in the circulation of blood.
3. Capillarity promotes the movement of ground water.
4. It is the principles on which paper and fabric towels work to absorb water.
5. Cotton clothing in hot climates uses capillarity action to draw perspiration away from the body.
6. In an oil or kerosene lamp capillarity draws the fuel up into the wicker where it can be burnt.
7. A writing Rubin splits in the middle so that a fine capillary is formed.

Osmosis

The Concept of Osmosis

Explain the concept of osmosis

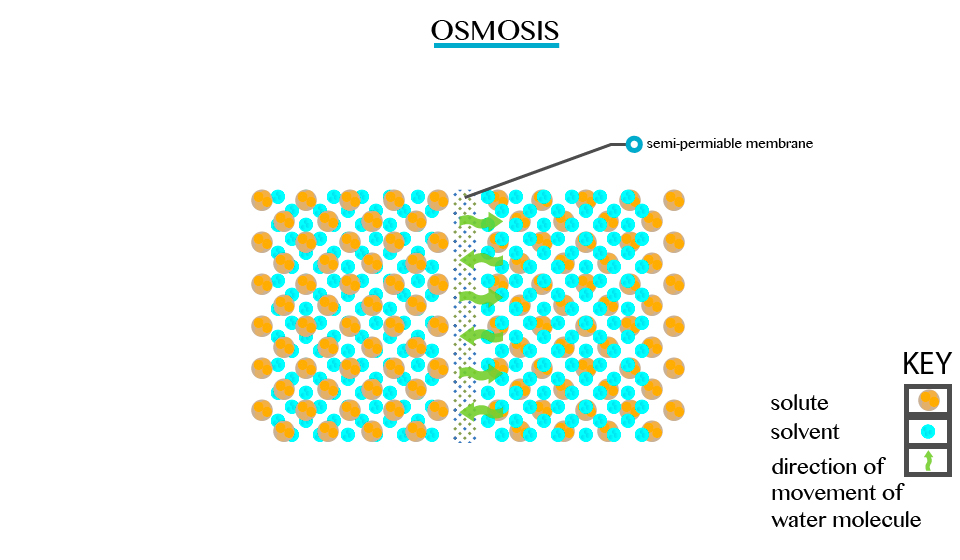
Defined as the movement of a solvent from a region of low concentration through semi permeable membrane.

Particles will diffuse through the membrane in an attempt to equalize the concentration on either side. E.g. two solutions of different concentration separated by a semi permeable membrane. The membrane is permeable to the smaller solvent molecules but not to the larger solute molecules. Osmosis stops when the concentration becomes the same on either side of the membrane.

Osmosis stops when the concentration becomes the same on either side of the membrane.

Applications of Osmosis in Daily Life

Identify the applications of osmosis in daily life

Applications of osmosis in daily life:

1. Control the movement of water and nutrients in and out of the cell.
2. Filtration processes.
3. Removal of harmful ingredients from dinking water.
4. Removing salt from seawater so as to make it suitable for drinking and for other domestic uses
5. Any other